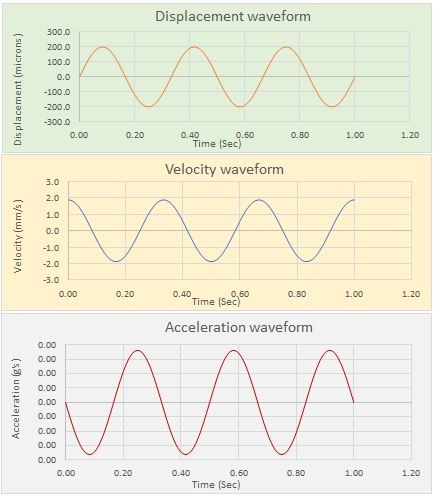
Let’s consider a sinusoidal (single discrete frequency) displacement waveform. it could be mathematically mentioned as,

X = D * sin (2πft)

Rate of change of displacement, ie Velocity, 

V           = d/dt (D * sin (2πft))

               = D * cos (2πft) * 2πf

               = 2πfD * cos (2πft)

Converting cosine wave into sine wave, {cos Φ = sin (90 + Φ)} 

V           = 2πfD * sin (2πft + 90)

Hence, If we know the displacement amplitude and frequency, then we can calculate using the formula V = 2πfD. Velocity signal with this maximum amplitude will lead the displacement signal by 90 deg.

(Additional note: The frequency here is the single discrete frequency. This conversion could not be performed for overall amplitude values)

Similarly,

A           = d/dt (2πfD * sin (2πft + 90))

               = 2πfD * cos (2πft + 90) * 2πf

               = (2πf)^2 * D * cos (2πft + 90)

Again, Converting cosine wave into sine wave,

A            = (2πf)^2 * D * sin (2πft + 90 + 90)

               = (2πf)^2 * D * sin (2πft + 180)

Or A      = 2πfV * sin (2πft + 90)

Acceleration leads displacement by 180 deg and velocity by 90 deg.

Generally, phase is mentioned as phase lag. Ie, the increase in phase angle value means increase in phase lag. Hence, to get phase angle for velocity signal from displacement, we should subtract it by 90 deg.

For example, if the phase angle of displacement signal is 100 deg, then phase angle of velocity and acceleration signal will be 10 deg and 280 deg respectively.